To go a step further with tips, I decided that since most of the people in our class are going to become teachers, I though it would also be important to share some tips on being a student teacher. I came across this article, and it has plenty of great tips for someone who is about to student teach. The article addresses everything from dress code to keeping a journal. I think one of the best tips in the list is the one about always being professional. It states that even though you may feel comfortable with your cooperating teacher, other teachers, or even some students, you must remember that you are a guest in their school and you must stay professional. The article can be found here: http://voices.yahoo.com/surviving-student-teaching-guide-coming-33040.html

Saturday, December 8, 2012
Hexaflexagons
Last week in my College Geometry class, we had to do a presentation on Origami. For the presentation we did the usual: history,origins, etc... However, when it came time for the group participation, we decided to use something that we saw in our Math Seminar class. I recalled a video that Dr. Milou showed us on hexaflexagons and thought that this would be a perfect example of origami to have the class make. So, my group members and I watched Vi Hart's video on YouTube, then made step-by-step instructions on how to make them.
To make the hexaflexagons, I was able to find templates online that were in color, and came pre-numbered. If the hexaflexagon was constructed properly, each "face" would display the same number, but with 2 alternating colors. When it cam time for the participation part, we just showed Vi Hart's video, but didn't tell our classmates until after the video that they would be making hexaflexagons too. Needless to say, those that have seen, or heard of, hexaflexagons were excited (I actually heard a few "yay's" when we told them). For the classmates that hadn't heard of hexaflexagons, by the time they were done constructing them, they were excited as well. Once they figured out how to flip and fold it to get to the different "faces", most of them couldn't put it down! The video to see what exactly a hexaflexagon is can be seen here: https://www.youtube.com/watch?v=VIVIegSt81k
Here are the steps to make a hexaflexagon using the template found on auntannie.com
To make the hexaflexagons, I was able to find templates online that were in color, and came pre-numbered. If the hexaflexagon was constructed properly, each "face" would display the same number, but with 2 alternating colors. When it cam time for the participation part, we just showed Vi Hart's video, but didn't tell our classmates until after the video that they would be making hexaflexagons too. Needless to say, those that have seen, or heard of, hexaflexagons were excited (I actually heard a few "yay's" when we told them). For the classmates that hadn't heard of hexaflexagons, by the time they were done constructing them, they were excited as well. Once they figured out how to flip and fold it to get to the different "faces", most of them couldn't put it down! The video to see what exactly a hexaflexagon is can be seen here: https://www.youtube.com/watch?v=VIVIegSt81k
Here are the steps to make a hexaflexagon using the template found on auntannie.com
- .Score and fold back and forth on all the solid lines. Do this for each of the 19 triangles of the
hexa-hexaflexagon.
Place the strip of 19 triangles with the side with 6s, 5s, and 4s face up and the glue tab, *, to the left. Fold the strip back on itself matching two 6s, then two 5s, then two 4s, on like this for the entire strip (nine folds). Now you have a strip of 10 triangles.

Place the strip with the side without glue tabs facing up and the 3 end to the left. Fold back on the line between the third and fourth triangles (2 and 1)—four 2s are together now. Fold back on the line between the next 2 and 1. Now you should be able to see five 2s. Pull the 2 forward that is behind the 3. There should be six 2s on top and a 1 to the side. Fold the 1 back.The two glue tabs marked with '*' are now face-to-face. Glue them together. Wait for the glue to dry before flexing your flexagon. - Step 6: Flex
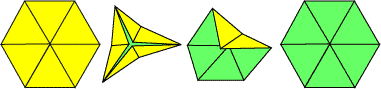
- Fold the flexagon to bring together three alternate corners of the flexagon. The top of the
flexagon will pop open if there is a new face to reveal. If it doesn't pop open, flatten the
flexagon and try again with the other three corners.
As you flex the flexagon in this project, see if you can find all the possible combinations of faces. The hexa-hexaflexagon has six faces with 3 different arrangements each, for a total of 18 possible faces. Only 15 of the faces versions can be seen with the straight strip pattern for a hexa-hexaflexagon. Can you find all 15 possibilities?
Tips For A New Math Teacher
Since most of the people in our class are going on to become a math teacher, I thought it would be fitting to find an article that gives some tips on what to do in the first year. Being that it is going to be overwhelming for any new teacher walking into the classroom, things may be forgotten, or just put on the back burner until the teacher gets their bearings. Instead of having a link to a webpage, I am just going to include them here. I think that the tips given in this particular article are solid, as they seem to highlight the important features for new math teachers. The article can be seen at: http://www.teachercertification.org/a/tips-for-math-teachers.html
I also found some other tips that I found quite amusing. The author (Davilla Riddle) has taken a Letterman-esque approach to tips for a new teacher. Even though some of these may be true, keep in mind that they are of a joking manor....
Letterman's Top 10 - Advice for New Teachers
10. Know where your room is located on campus. It helps when you are coming back to your room from a fire drill at the beginning of the year - don't want to get lost.
9.Know who is really "in charge" at the front office - the principal's administrative assistant.
8. Find out what goodies the custodians like to eat. They can be your best friend or your worst enemy.
7. Learn your kids' names. Middle schoolers hate being called by the "wrong" name.
6. Find a partner in crime (fellow teacher) to give you the scoop on what's really going on at school.
5. Make friends with the counselor. He/she can really be a great ally during a heated parent/teacher conference.
4. Don't ask your kids too many questions. You never know what they are going to say...sometimes, it is TMI (too much information).
3. Don't try to be a super hero by volunteering for everything. There is always next year!
2. If it isn't locked away, taped down or glued to the wall - it will be gone or destroyed by the end of the year.
1. Get a degree in "How to Fix the Copier". It will come in handy on Monday mornings when you are running late to make copies for class.
I also found some other tips that I found quite amusing. The author (Davilla Riddle) has taken a Letterman-esque approach to tips for a new teacher. Even though some of these may be true, keep in mind that they are of a joking manor....
Letterman's Top 10 - Advice for New Teachers
10. Know where your room is located on campus. It helps when you are coming back to your room from a fire drill at the beginning of the year - don't want to get lost.
9.Know who is really "in charge" at the front office - the principal's administrative assistant.
8. Find out what goodies the custodians like to eat. They can be your best friend or your worst enemy.
7. Learn your kids' names. Middle schoolers hate being called by the "wrong" name.
6. Find a partner in crime (fellow teacher) to give you the scoop on what's really going on at school.
5. Make friends with the counselor. He/she can really be a great ally during a heated parent/teacher conference.
4. Don't ask your kids too many questions. You never know what they are going to say...sometimes, it is TMI (too much information).
3. Don't try to be a super hero by volunteering for everything. There is always next year!
2. If it isn't locked away, taped down or glued to the wall - it will be gone or destroyed by the end of the year.
1. Get a degree in "How to Fix the Copier". It will come in handy on Monday mornings when you are running late to make copies for class.
When Am I Ever Going To Use This?
The question above is a question that has probably been around since the dawn of mathematics. This is a question that I'm sure has been posed to every math teacher that teaches middle/high school and college mathematics. The answer is not quite to easy to give. It all depends on the material being learned, and if the teacher can come up with a legitimate answer. I have found, through the article posted below, that there really isn't one specific reason that a teacher can give to answer this question.
In the article below, the author goes through a series of examples, and takes some common answers and explains why they may not be the best answers to use. First of all, if a specific job is named, and the student has not intention going into that field, you just lost him. If the real-world relation you gave to answer the question seems too complicated, you lost him again. The article goes into detail on how NOT to answer the question so that you won't lose your students. It does not, however, give the exact reason you should give to your students. It does give tips on how to approach the question, but in the end, you need to come up with the best answer you can.
The article does go on to say that the student may not ever use the specific topic in everyday life, but the actual processes that go along with that topic are ones that are used in everyday life. For an example, you need to have problem-solving skills to do most mathematical topics, and problem-solving skills are definitely a need for everyday life. I think the author actually does a great job on explaining why some of the common answers aren't good ones as they can make the teacher appear foolish, uninterested, or even giving the student a negative attitude towards mathematics.
In addition to the article, I have also posted a poster that I saw in a mathematics classroom where I was substituting, and I actually think that EVERY mathematics classroom should have this poster. The poster gives a list of many different types of jobs on the top, and along the side it shows what types of mathematics are needed to do that job.
Article: http://blog.mrmeyer.com/wp-content/uploads/Otten_2011MT_reprint.pdf
In the article below, the author goes through a series of examples, and takes some common answers and explains why they may not be the best answers to use. First of all, if a specific job is named, and the student has not intention going into that field, you just lost him. If the real-world relation you gave to answer the question seems too complicated, you lost him again. The article goes into detail on how NOT to answer the question so that you won't lose your students. It does not, however, give the exact reason you should give to your students. It does give tips on how to approach the question, but in the end, you need to come up with the best answer you can.
The article does go on to say that the student may not ever use the specific topic in everyday life, but the actual processes that go along with that topic are ones that are used in everyday life. For an example, you need to have problem-solving skills to do most mathematical topics, and problem-solving skills are definitely a need for everyday life. I think the author actually does a great job on explaining why some of the common answers aren't good ones as they can make the teacher appear foolish, uninterested, or even giving the student a negative attitude towards mathematics.
In addition to the article, I have also posted a poster that I saw in a mathematics classroom where I was substituting, and I actually think that EVERY mathematics classroom should have this poster. The poster gives a list of many different types of jobs on the top, and along the side it shows what types of mathematics are needed to do that job.
Article: http://blog.mrmeyer.com/wp-content/uploads/Otten_2011MT_reprint.pdf
Technology Can Be Fun
Technology in the classroom these days is a must. However, it doesn't have to be the newest calculator, the fun software, or even the newest gadget. Sometimes the technology that can teach students, or further their understanding is something they probably use every day, the internet. Granted, there are many helpful math sites that students can go on to find information, but that may not be that helpful. A new trend that is going on is uploading fun math videos to YouTube.
Since most people are familiar with YouTube, it is something that can be accessed with little trouble. Not only are the videos entertaining, but they are made to get the point of the lesson across. The videos I have posted below are only a few examples of what can be found on You Tube. You can find anything from counting by one's to finite simple groups. This is just another way to incorporate technology into the classroom, but it also is a lighthearted way to introduce a new concept.
The videos I mentioned can be found here:
https://www.youtube.com/watch?v=BipvGD-LCjU
https://www.youtube.com/watch?v=94QHaAPPzac
https://www.youtube.com/watch?v=CoxNc-atJ14
https://www.youtube.com/watch?v=-b2xUb0VofQ
https://www.youtube.com/watch?v=TYsWIWckKeg
Since most people are familiar with YouTube, it is something that can be accessed with little trouble. Not only are the videos entertaining, but they are made to get the point of the lesson across. The videos I have posted below are only a few examples of what can be found on You Tube. You can find anything from counting by one's to finite simple groups. This is just another way to incorporate technology into the classroom, but it also is a lighthearted way to introduce a new concept.
The videos I mentioned can be found here:
https://www.youtube.com/watch?v=BipvGD-LCjU
https://www.youtube.com/watch?v=94QHaAPPzac
https://www.youtube.com/watch?v=CoxNc-atJ14
https://www.youtube.com/watch?v=-b2xUb0VofQ
https://www.youtube.com/watch?v=TYsWIWckKeg
Start Them Young
Have you ever heard someone say "I'm just not good at math"? Well, my personal experience has shown me that a lot of people feel that way. However, they may not be able to master calculus, but everyone is a master at math in their own way. The thing is, math skills start at a very young age. Children are very impressionable, and are susceptible to taking on the same attitude about a subject as their parent if they have been exposed to it. This can be completely detrimental to a child's development. So, as I was wandering around the internet, I found this article (see below) that piqued my interest.
The article explains how that starting to teach a child math at a younger age can help them in the long run. It also makes a good point that most children are encouraged to read, and that their parents will sit with them and read to them, or with them. But how often do you hear of a parent that sits down with their child to learn math? That's exactly what this article talks about. It shows that things that may be meaningless to an adult, can be beneficial to a child. What I mean is this, such simple things as counting, or learning different shapes can help a child's math skills. Statements to this effect are also mentioned in the article.
I will say that I was one of those people. I thought I stunk at math, but after I graduated high school and started working, I realized that I actually enjoyed working with numbers (I worked as a mortgage processor for over 10 years). Being that most jobs require some type of math skills, it is imperative that children be taught these skills as well. The article is more focused towards parents with young children, but it shows that even just a little time spent learning some basic math skills can only help their development.
To view the article, click here: http://www.pbs.org/parents/education/math/math-tips-for-parents/instill-a-love-of-math/
The article explains how that starting to teach a child math at a younger age can help them in the long run. It also makes a good point that most children are encouraged to read, and that their parents will sit with them and read to them, or with them. But how often do you hear of a parent that sits down with their child to learn math? That's exactly what this article talks about. It shows that things that may be meaningless to an adult, can be beneficial to a child. What I mean is this, such simple things as counting, or learning different shapes can help a child's math skills. Statements to this effect are also mentioned in the article.
I will say that I was one of those people. I thought I stunk at math, but after I graduated high school and started working, I realized that I actually enjoyed working with numbers (I worked as a mortgage processor for over 10 years). Being that most jobs require some type of math skills, it is imperative that children be taught these skills as well. The article is more focused towards parents with young children, but it shows that even just a little time spent learning some basic math skills can only help their development.
To view the article, click here: http://www.pbs.org/parents/education/math/math-tips-for-parents/instill-a-love-of-math/
Calculators: Good Or Bad?
Being that technology is an ever-present part of our society, it has also become part of the mathematics classroom. From calculators, basic ones (4-function) to ones that use Computer Algebra Systems (graphing calculators) to software such as Geometer's Sketchpad, the use of technology is being implemented increasingly in today's classrooms. However, there is much debate on whether the technology helps or hurts students. In the attached article, this topic of debate is discussed with research to back it up.
The article is about studies that have been conducted to show if calculators are helpful or detrimental to students. It explains that some hesitancy comes from fear, as well as ignorance of not knowing how to use them. It also gives parameters of certain studies done, as well as their results. The article does show that not only can students benefit from calculators, but they can also develop a better attitude towards mathematics. The article also mentions that the standard pencil-and-paper method can be enhanced with the use of a graphing calculator, and that understanding of concepts can deepen with a calculator. Since one of the bigger concerns in the classroom are achievement tests, this article reports that scores on achievement tests for algebra and calculus are higher with the use of a calculator.
I found this article pretty fascinating, since I wasn't introduced to a graphing calculator until I reached college. That may also be due, in part, to the fact that I graduated high school in 1996 when technology wasn't emphasized nearly as much as it is today. In my personal opinion, I do think that calculators can only help in the classroom. Not only do they help cut down on time spent doing long calculations, but actually being able to see the result helped me understand graphs better.
To view the article, click here: http://mathforum.org/technology/papers/papers/dunham.html
The article is about studies that have been conducted to show if calculators are helpful or detrimental to students. It explains that some hesitancy comes from fear, as well as ignorance of not knowing how to use them. It also gives parameters of certain studies done, as well as their results. The article does show that not only can students benefit from calculators, but they can also develop a better attitude towards mathematics. The article also mentions that the standard pencil-and-paper method can be enhanced with the use of a graphing calculator, and that understanding of concepts can deepen with a calculator. Since one of the bigger concerns in the classroom are achievement tests, this article reports that scores on achievement tests for algebra and calculus are higher with the use of a calculator.
I found this article pretty fascinating, since I wasn't introduced to a graphing calculator until I reached college. That may also be due, in part, to the fact that I graduated high school in 1996 when technology wasn't emphasized nearly as much as it is today. In my personal opinion, I do think that calculators can only help in the classroom. Not only do they help cut down on time spent doing long calculations, but actually being able to see the result helped me understand graphs better.
To view the article, click here: http://mathforum.org/technology/papers/papers/dunham.html
Have Fun With Your Students
Since the last few entries on my blog have been about my research paper, I wanted to change it up a little bit. I'm sure that not everyone wants to read about how fractals are being used in medicine, so I thought I'd take a different direction with this post. I wanted to show that teaching math doesn't always have to be boring and mundane. Teachers are always thinking of creative ways to get the students to understand the material. Not only do teachers have to be creative, but they have to make sure that they are getting the point across. As I was searching YouTube, I came across a video that showed me how creative some teachers can be, and how they are willing to go the extra mile in the classroom.
This video (https://www.youtube.com/watch?v=XKviYiZhtZY) shows a teacher explaining a problem regarding 1=2, and uses plenty of different tactics for the students to understand the problem. Granted, the steps of the teacher completing the problem have been skipped over, but the way he uses himself as an example is quite interesting. I also chose this video because it also shows that teachers can have some fun with the students, and that teachers are also willing to let loose, and go with the flow. The video was shot around Halloween, and it just shows how the teacher got into the spirit of the holiday, all while giving a lesson.
This video (https://www.youtube.com/watch?v=XKviYiZhtZY) shows a teacher explaining a problem regarding 1=2, and uses plenty of different tactics for the students to understand the problem. Granted, the steps of the teacher completing the problem have been skipped over, but the way he uses himself as an example is quite interesting. I also chose this video because it also shows that teachers can have some fun with the students, and that teachers are also willing to let loose, and go with the flow. The video was shot around Halloween, and it just shows how the teacher got into the spirit of the holiday, all while giving a lesson.
Subscribe to:
Comments (Atom)
